Las parábolas, conceptos básicos.
Definición de parábola.
Se dice que una parábola es, el lugar geométrico de los puntos \(P(x,\ y)\) del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz, donde el foco no está sobre la directriz.
 La distancia del foco al punto de apertura de la parábola llamado vértice es igual a la distancia del punto de apertura a la recta, recibe el nombre de parámetro y se denota por la letra \(p\).
La distancia del foco al punto de apertura de la parábola llamado vértice es igual a la distancia del punto de apertura a la recta, recibe el nombre de parámetro y se denota por la letra \(p\).
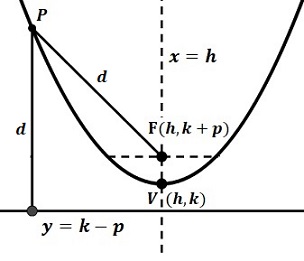
En la gráfica se muestra una parábola cuyo foco es el punto \(F=(h,k+p),\) y la directriz es la recta \(y=k-p.\) El segmento que une el punto \(P\) con el foco se denomina radio vector o radio focal.
El punto de apertura es llamado “vértice” y se representa por el punto \(V(h,k),\) es el punto más bajo de ella (mínimo) si abre hacia arriba, en cambio si abre hacia abajo es el punto más alto (máximo), este se se encuetra sobre la misma recta que el foco, llamada eje de la parábola el cual es la recta perpendicular a la diretriz que pasa por el vértice, recta \(x=h\) de la figura.
Un segmento que toca dos puntos de la parábola se denomina cuerda. Una cuerda que pasa por el foco y es perpendicuar al eje de simetría, se denomina lado recto y tiene una longitud de cuatro veces el valor absoluto del parámetro, esto es \(l=\left|4p\right|\).
Ecuaciones y gráficas.
Ecuación de la parábola con vértice en el punto \((0,0)\).
Para iniciar considere la gráfica de la parábola más sencilla, vértice en el punto \((0,\ 0),\) foco en el punto \((0,\ p)\) y de directriz la recta \(y=-p.\)
De la definición de la parábola para un punto cualquiera \(P(x,y)\) las distancia \(d\left(P,\ F\right)=d\left(P,\ R\right)\) donde \(R=(x,0)\) (ver la figura de arriba) de esto se deduce:
\begin{align}
&\sqrt{\left(x-0\right)^2+\left(y-p\right)^2}=\ \sqrt{\left(x-x\right)^2+\left(y+p\right)^2}~~~~~~~~~~~~~~\mathrm{Definición~ de~ parábola.}\\
&\sqrt{x^2+\left(y-p\right)^2}=\sqrt{\left(y+p\right)^2}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando~ expresiones.}\\
&x^2+\left(y-p\right)^2=\left(y+p\right)^2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Elevando~ al ~cuadrado.}\\
&x^2+y^2-2py+p^2=y^2+2py+p^2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{ Desarrollando ~potencias.}\\
&x^2=4py ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando~ y~ agrupando.}\\
\end{align}
esta es la forma más simple para la ecuación de una parábola cuyo eje es vertical. De manera análoga puede demostrarse que la ecuación de la parábola con vértice en \((0,\ 0)\) cuyo eje es la reta \(y=0\) es \(y^2=4px.\)
Ecuaciones reducidas de la parábola
$${4py=x}^2~~~~~~ {\rm ó}~~~~~~ 4px=y^2$$
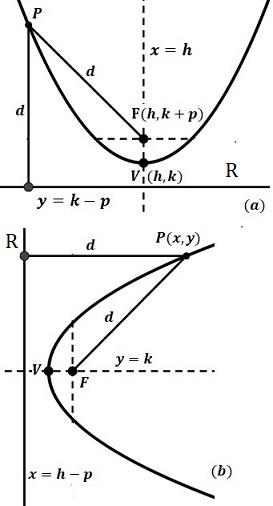 Ecuación de la parábola con vértice en el punto \(V(h,k)\).
Ecuación de la parábola con vértice en el punto \(V(h,k)\).
Considere de nuevo la figura de más arriba, en ella se presenta una parábola cuyo vértice es el punto \(V(h,k)\) y su foco es \(F(h,k+p)\). Por definición de la parábola es igual al conjunto de todos los puntos \(P(x,y)\) tales que la distancia del punto al foco \(d(P,F)\) es igual a la distancia del punto a la recta directriz \(d(P,R)\), esto es
$$d(P,F)=d(P,R)$$
De esta afirmación, analíticamente al sustituir cada uno de los elementos que intervienen en la definción por su valor se deducen a través del analisis algebraico las ecuaciones de la parábola.
\begin{align}
&\sqrt{\left(x-h\right)^2+\left(y-(k+p)\right)^2}=\sqrt{\left(x-x\right)^2+\left(y-(k-p)\right)^2}\\
&\sqrt{\left(x-h\right)^2+\left(y-k-p\right)^2}=\sqrt{\left(y-k+p\right)^2}~~~~~~\mathrm{Simplificando.}\\
&\left(x-h\right)^2+\left(y-k-p\right)^2=\left(y-k+p\right)^2 ~~~~~~~~~~~~~~\mathrm{Simplificando.}\\
&\left(x-h\right)^2+y^2-2ky-2py+2kp+k^2+p^2=y^2+2py-2ky-2kp+k^2+p^2\\
&\left(x-h\right)^2=4py-4kp~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando.}\\
&\left(x-h\right)^2=4p(y-k)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Factorizando.}\\
\end{align}
que es la ecuación de la parábola con vértice en el punto \(h,k)\) y eje \(x=h\).
De manera análoga puede demostrarse que la ecuación de la parábola con vértice en \((h,k)\) y eje \(y=k\) es \((y-k)^2=4p(x-h)\). En la tabla de más abajo se muestran las propiedades analíticas de ambas ecuaciones.
Ecuaciones de la parábola
\[\begin{array}{c|c|c|c|c|c} {\rm Ecuación ~cartesiana}& {\rm Vértice}& {\rm Eje}& {\rm Foco}& {\rm Directriz}& {\rm Abre~ para}\\ \hline {(x-h)}^2=4p(y-k)& (h,k)& x=h& (h,k+p)& y=k-p&{\rm arriba ~si}~ p>0\\ \hline {(y-k)}^2=4p(x-h)& (h,k)& y=k& (h+p,k)& x=h-p& {\rm derecha ~si}~ p>0\\ \hline\hline\end{array}\] En forma estándar la ecuación \((x-h)^2=4p(y-k)\) se escribe para \(a=1/4p\) como,
Forma estándar
$$y=a(x-h)^2+k$$
Para más contenidos y luego clic en la pestaña del contenido deseado.
La parábola como función cuadrática.
Una función cuadrática es, una función del tipo \(y=ax^2+bx+c\) o \(f(x)=ax^2+bx+c\) donde \(a\neq0,\) si \(a=0\) la función es lineal.
Ahora bien, la ecuación \(y=ax^2+bx+c\) es una ecuación equivalente a \({(x-h)}^2=4p(y-k)\) la cual se escribe en la forma estándar o normal como \(y=a\left(x-h\right)^2+k\) haciendo \(a=1/4p\) (ver los conceptos básicos), esta manera de escribir la ecuación de una parábola resulta muy útil, pues muestra información directa sobre el vértice \((h,k)\) de la parábola y el valor del parámetro \(p\), además facilita el estudio analítico y gráfico de las parábolas como funciones cuadráticas.
Gráficas de funciones cuadráticas (parábolas).
Otro punto importante en el estudio de las funciones cuadráticas son sus gráficas. La gráfica de una función cuadrática describe precisamente la curva llamada parábola.
La manera más fácil de realizar una gráfica de cualquier función matemática es utilizar un programa de graficación que sea capaz de mostrar con claridad los detalles de esta, sin embargo, para la compresión y realización de un buen bosquejo a mano de la gráfica de una parábola, se recomienda conocer un mínimo de cinco o seis puntos por donde pase la gráfica. Los puntos más convenientes para este fin son deducidos analíticamente como sigue:
1. Vértice \((h,k)\) de la parábola, $$\left(h,k\right)=\left(-\frac{b}{2a},f\left(-\frac{b}{2a}\right)\right)$$
2. Intersecciones en eje de abscisas (eje\(x\)), puntos para los cuales \(ax^2+bx+c=0\) en \(\mathbb{R}.\) Si \(ax^2+bx+c=0\) no tiene solución en \(\mathbb{R}\) no hay intersección conel eje \(x\).
3. Intersección en eje de ordenadas eje \(y\)
Hacer \(x=0\) en \(y=ax^2+bx+c\) de donde se tiene el punto \((0,c)\)
4. Determinar las coordenadas de dos o más puntos evaluando la expresión cuadrática \(y=ax^2+bx+c.\) Los valores más convenientes son \(x_1=h-x\) al junto de \(x_2=h+x\)
5. Unir todos los puntos con una curva suave.
Como se podrá notar, realizar un bosquejo de una función cuadrática no conlleva un desafío mayor a la resolución de una ecuación cuadrática, para lo cual puede usar el método de su preferencia.
Valores máximos y mínimos de la parábola.
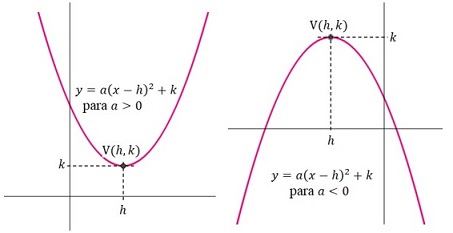 Antes de bosquejar la gráfica de una función cuadrática se debe considerar algunas características importantes de esta como se muestra en la figura, observar con detenimiento algunos detalles, ahorrará tiempo y esfuerzo.
Antes de bosquejar la gráfica de una función cuadrática se debe considerar algunas características importantes de esta como se muestra en la figura, observar con detenimiento algunos detalles, ahorrará tiempo y esfuerzo.
1. El máximo o mínimo siempre ocurre en el punto \((h,k)\).
2. Si \(a>0\) la parábola abre hacia arriba y \((h,k)\) es mínimo.
3. Si \(a< 0\) la parábola abre hacia abajo y \((h,k)\) es máximo.
Amplitud de la gráfica en una parábola.
Al escribir \(y=a{(x-h)}^2+k\) o como un trinomio \(y=ax^2+bx+c\) el valor \(a\) representa además del resultado ya conocidos (sentido de apertura), la amplitud de la parábola, y de esto se pueden realizar otras tres afirmaciones importantes más:
1. Cuanto más cerca esté el \(\left|a\right|\) de cero, la parábola es más abierta.
2. Cuanto más cerca esté el \(\left|a\right|\) de uno, la parábola es más cercana a la gráfica de \(y=x^2\) desplazada.
3. Cuanto más lejos esté el \(\left|a\right|\) de uno, la parábola es más cerrada, y ambas “ramas” se acercan más al eje de ordenada.
 Ejemplo 1. Realizar un bosquejo de las gráficas de: \(1.~~ f\left(x\right)=x^2~~~~ 2.~~f\left(x\right)=-x^2\)
Ejemplo 1. Realizar un bosquejo de las gráficas de: \(1.~~ f\left(x\right)=x^2~~~~ 2.~~f\left(x\right)=-x^2\)
Solución: comparando \(y=x^2\) con la forma \(y=a\left(x-h\right)^2+k\) se tiene que \(a=1\), por tanto, abre para arriba. \(h=0; \ k=0\) de donde el vértices es \(V=(0,0).\)
Comparando \(y=-x^2\) con la forma \(y=a\left(x-h\right)^2+k\) se tiene \(a=-1\), por tanto, abre para abajo.
Además \(h=0; \ k=0\) de donde el vértice es el punto \(V=(0,0).\)
La solución se muestra en la gráfica de la izquierda.
Partiendo de la gráfica de la función \(y=x^2\) se pueden realizar varias transformaciones y desplazamientos a esta gráfica dando origen a muchas otras formas las cuales se presentan a continuación en forma de tabla.
Transformaciones básicas a la gráfica de \(y=x^2\)
\begin{array}{l l} {\rm Gráfica}&{\rms Dezplazamiento}\\ y=x^2& {\rm Gráfica ~original.}\\ y=x^2+k & k ~{\rm unidades~ hacia~ arriba.}\\ y=x^2-k&k ~{\rm unidades ~hacia ~abajo.}\\ y=(x-h)^2& h~ {\rm unidades~ hacia~ la derecha.}\\ y=(x+h)^2&h ~{\rm unidades ~hacia~ la~ izquierda}\\ y=(x-h)^2+k& {\rm Dezplazaminto ~horizontal~ y ~vertical}\\ y=a(x-h)^2+k&{\rm Amplitud}~ a~ {\rm ~y ~desplazamiento~ horizontal~ y~ vertical.}\end{array} Además, si \(a< 0\) hay un cambio de sentido en la parábola como se ve en la figura de arriba. Este y otros hechos se muestran a continuación, en los siguientes ejemplos.
Para más contenidos y luego clic en la pestaña del contenido deseado.
tab-15
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
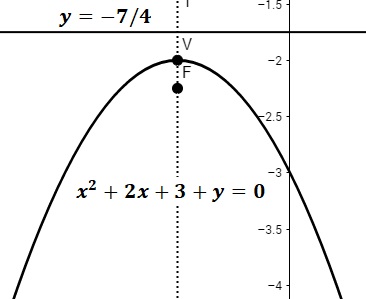
Dada la parábola \(x^2+2x+3+y=0\) determinar hacia donde abre, el vértice, el foco, la directriz y el eje de simetría.
Determinar la ecuación de la parábola cuyo eje de simetría es horizontal, con vértice en el punto \(V\left(-5,1\right)\) y que pasa por el punto \(P\left(-1,0\right)\).
Dadas las funciones \(f(x)=2(x-5)^2+8\) y \({\rm g}(x)=-12(x+3)^2-4\) determinar las coordenadas del vértice, el valor del parámetro \(p\) y el valor mínimo (o máximo).
Dada \(f(x)=4x^2-24x+39\) escribir la ecuación en forma normal, determinar el valor del parámetro \(p\), las coordenadas del vértice estableciendo si es máximo o mínimo.
Lugar geométrico. Determinar la ecuación del lugar geométrico de los puntos cuyas distancias no dirigidas a \((5,\ 0)\) son iguales a sus distancias no dirigidas a la recta \(x+ 5=0.\)
Una recta que pasa por el foco de una parábola con vértice en el origen y con eje horizontal, corta a la directriz en el punto \((-3,\ 8)\). Calcular las coordenadas de los puntos de intersección de la parábola y la recta.
Dados los puntos \(A(2,\ 4)\) y \(B(5,\ -3).\) Determinar el lugar geométrico de los puntos \(P(x,\ y)\) de manera que la pendiente de \(PA\) sea igual a la pendiente de \(PB,\) más la unidad.
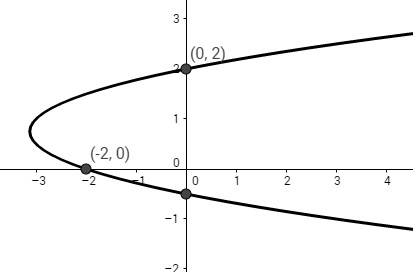
Determinar la ecuación de una parábola cuya directriz es vertical y pasa por los puntos \(\left(0,\ 2\right),(-2,0)\) y \(\left(0,\ 1/2\right)\).

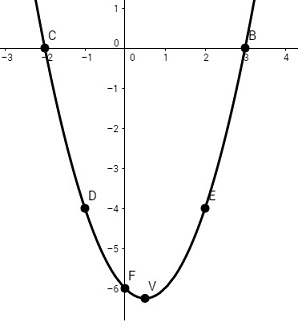 5. Unir con una curva suave todos los puntos encontrados (como se muestra en la figura de la derecha).
5. Unir con una curva suave todos los puntos encontrados (como se muestra en la figura de la derecha).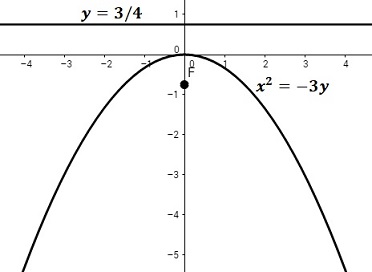
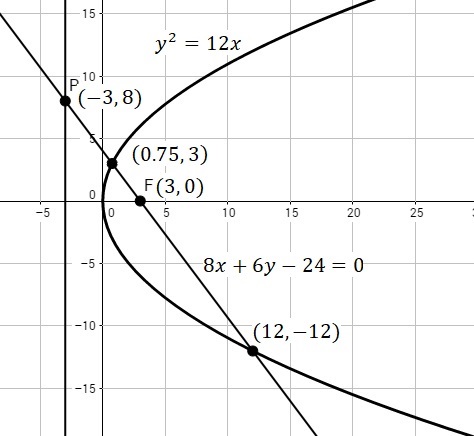 los puntos \((3/4,3)\) y \((12,-12)\) son los puntos de intersección.
los puntos \((3/4,3)\) y \((12,-12)\) son los puntos de intersección.